Design avfotoniskIntegrert krets
Fotoniske integrerte kretsløp(PIC) er ofte designet ved hjelp av matematiske skript på grunn av viktigheten av banelengde i interferometre eller andre applikasjoner som er følsomme for banelengde.Bildeer produsert ved å mate flere lag (vanligvis 10 til 30) på en skive, som er sammensatt av mange polygonale former, ofte representert i GDSII -formatet. Før du sender filen til Photomask -produsenten, er det sterkt ønskelig å kunne simulere PIC for å bekrefte riktigheten av designet. Simuleringen er delt inn i flere nivåer: det laveste nivået er den tredimensjonale elektromagnetiske (EM) simuleringen, der simuleringen utføres på underbølgelengde-nivå, selv om interaksjonene mellom atomer i materialet blir håndtert i den makroskopiske skalaen. Typiske metoder inkluderer tredimensjonal endelig-forskjellstidsdomene (3D FDTD) og EigenMode Expansion (EME). Disse metodene er de mest nøyaktige, men er upraktiske for hele PIC -simuleringstiden. Det neste nivået er 2,5-dimensjonal EM-simulering, for eksempel endelig forskjellsstråleutbredelse (FD-BPM). Disse metodene er mye raskere, men ofrer litt nøyaktighet og kan bare håndtere paraxial forplantning og kan for eksempel ikke brukes til å simulere resonatorer. Neste nivå er 2D EM -simulering, for eksempel 2D FDTD og 2D BPM. Disse er også raskere, men har begrenset funksjonalitet, slik at de ikke kan simulere polarisasjonsrotatorer. Et ytterligere nivå er overføring og/eller spredningsmatrikssimulering. Hver hovedkomponent reduseres til en komponent med inngang og utgang, og den tilkoblede bølgelederen reduseres til et faseskift og dempningselement. Disse simuleringene er ekstremt raske. Utgangssignalet oppnås ved å multiplisere overføringsmatrisen med inngangssignalet. Spredningsmatrisen (hvis elementer kalles S-parametere) multipliserer inngangs- og utgangssignalene på den ene siden for å finne inngangs- og utgangssignalene på den andre siden av komponenten. I utgangspunktet inneholder spredningsmatrisen refleksjonen inne i elementet. Spredningsmatrisen er vanligvis dobbelt så stor som transmisjonsmatrisen i hver dimensjon. Oppsummert, fra 3D EM til overføring/spredningsmatrikssimulering, presenterer hvert lag simulering en avveining mellom hastighet og nøyaktighet, og designere velger riktig simuleringsnivå for deres spesifikke behov for å optimalisere designvalideringsprosessen.
Å stole på elektromagnetisk simulering av visse elementer og bruke en sprednings-/overføringsmatrise for å simulere hele PIC garanterer ikke en helt korrekt design foran strømningsplaten. For eksempel beregnet feilkalkulerte banelengder, multimode-bølgeledere som ikke klarer å undertrykke høye ordens modus, eller to bølgeledere som er for nær hverandre, noe som fører til uventede koblingsproblemer, vil sannsynligvis bli uoppdaget under simulering. Selv om avanserte simuleringsverktøy gir kraftige designvalideringsevner, krever det fremdeles en høy grad av årvåkenhet og nøye inspeksjon av designeren, kombinert med praktisk erfaring og teknisk kunnskap, for å sikre nøyaktigheten og påliteligheten av designen og redusere risikoen for strømningsarket.
En teknikk kalt sparsom FDTD lar 3D- og 2D FDTD -simuleringer utføres direkte på et komplett PIC -design for å validere designet. Selv om det er vanskelig for noe elektromagnetisk simuleringsverktøy å simulere en veldig stor skala, er det sparsomme FDTD i stand til å simulere et ganske stort lokalt område. I tradisjonell 3D FDTD begynner simuleringen med å initialisere de seks komponentene i det elektromagnetiske feltet i et spesifikt kvantisert volum. Etter hvert som tiden går, beregnes den nye feltkomponenten i volumet, og så videre. Hvert trinn krever mye beregning, så det tar lang tid. I sparsom 3D FDTD, i stedet for å beregne på hvert trinn på hvert punkt i volumet, opprettholdes en liste over feltkomponenter som teoretisk kan samsvare med et vilkårlig stort volum og bare beregnes for disse komponentene. På hvert tidstrinn legges punkter ved siden av feltkomponenter, mens feltkomponenter under en viss kraftterskel blir droppet. For noen strukturer kan denne beregningen være flere størrelsesordener raskere enn tradisjonell 3D FDTD. Sparsomme FDTD -er fungerer imidlertid ikke bra når du arbeider med spredende strukturer fordi dette tidsfeltet sprer seg for mye, noe som resulterer i lister som er for lange og vanskelige å administrere. Figur 1 viser et eksempelskjermbilde av en 3D FDTD -simulering som ligner på en polarisasjonsstrålesplitter (PBS).
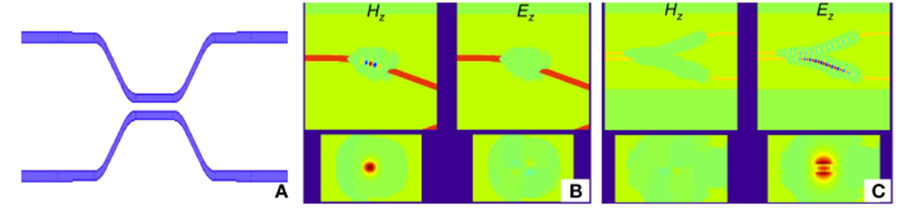
Figur 1: Simuleringsresultater fra 3D sparsom FDTD. (A) er en toppvisning av strukturen som blir simulert, som er en retningsbestemt kobling. (B) viser et skjermbilde av en simulering ved bruk av Quasi-TE-eksitasjon. De to diagrammer over viser toppvisningen av kvasi-te- og kvasi-TM-signalene, og de to diagrammer nedenfor viser det tilsvarende tverrsnittsvisningen. (C) viser et skjermbilde av en simulering ved bruk av Quasi-TM-eksitasjon.
Post Time: Jul-23-2024